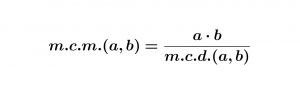Màxim divisor propi
Què es fer matemàtiques?
Si busquem una mica per Internet, podem trobar que: la matemàtica és aquella ciència que estudia patrons en les estructures de cossos abstractes i en les relacions que s’estableixen entre aquests. Encara que tinguen múltiples usos en altres disciplines, i tracti relacions que poden semblar evidents, les matemàtiques primer postulen, i després dedueixen i demostren.
Per un altre costat també trobem que: Les matemàtiques són un conjunt de coneixements associats en una primera aproximació als nombres i les formes, que progressivament es completen fins a constituir una manera valuosa d’analitzar situacions diverses. Permeten estructurar el coneixement que s’obté de la realitat, analitzar-la i aconseguir-ne una nova informació per conèixer-la millor, valorar-la i prendre decisions.
Considerem la següent situació:
Escriu tots els nombres naturals divisors de 9, 24, 36, 60, 74, 81, 37
Divisors de 9 = { 1, 3, 9 }
Divisors de 24 = { 1, 2 , 3, 4, 6, 8, 12, 24 }
Divisors de 36 = { 1, 2 , 3 , 4, 6, 9, 12, 18, 36 }
Divisors de 60 = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 }
Divisors de 74 = { 1, 2, 37, 74 }
Divisors de 81 = { 1, 3, 9, 27, 81 }
Divisors de 37 = { 1, 37 }
Quin és el major divisor propi de cada un, quan parlem de divisor propi l’excloem a ell mateix.
Major_Divisor de 9 = { 3 }
Major_Divisor de 24 = { 12 }
Major_Divisor de 36 = { 18 }
Major_Divisor de 60 = { 30 }
Major_Divisor de 74 = { 37 }
Major_Divisor de 81 = { 27 }
Major_Divisor de 37 = { 1 }
I, si observem una mica els resultats, podem deduir que en cap d’ells el major divisor propi que tenen supera a la meitat del nombre.
Aleshores podríem postular que:
«El major divisor propi de qualsevol nombre natural no podrà superar mai a la meitat d’aquest nombre.»
Aleshores anem a demostrar-ho per reducció al absurd, que no és més que suposar que no es compleix aquest postulat i veure que arribem a un impossible.
Tenim un nombre natural q que podem dividir en una quantitat de grups major a la seua meitat: d.
Per exemple tenim una quantitat de pedres molt gran «q» i anem a repartir-les en sacs. Les repartirem en «d» sacs que és una quantitat major que la meitat de «q».
Aleshores, suposem que en cada sac posem una pedra:
<< Aleshores al tindre una pedra en cada sac i com hi ha q pedres necessitarem q sacs, lo qual significaria que q coincideix amb d i per tant d no seria un divisor propi de q>>
Suposem ara que en cada sac posem dos pedres:
<< Aleshores tindríem que totes les pedres s'han repartit en d sacs on hem posat dues pedres en cadascú. Per tant, observar que si podem posar dos pedres en cada sac, es necessitarà una quantitat de sacs que serà la meitat de pedres que tenim. Aleshores tindrem que d és la meitat de q. I eixe resultat no és vàlid perquè d ha de ser un divisor de q major de la meitat d'aquest.>>
Suposem que en cada sac posem tres o més pedres:
<< Però si al repartir les q pedres en sacs on només caben dos, i també repartim les pedres on posem més de dos. Necessàriament la quantitat de sacs que emprem per a col·locar dues pedres serà major que la quantitat de sacs que necessitem per a col·locar tres o més pedres. Lo qual significa que d necessàriament ha de ser menor que la meitat de q>>.
I així arribem a un absurd, ja que necessàriament «d» ha de ésser menor que la meitat de q.
I per tant no hi ha cap divisor propi d’un nombre natural que supere la meitat d’aquest nombre.