diciembre 29

Semblança de triangles

SEMBLANÇA DE TRIANGLES.



Dos triangles són semblants si tenen els tres angles iguals i els tres costats proporcionals.



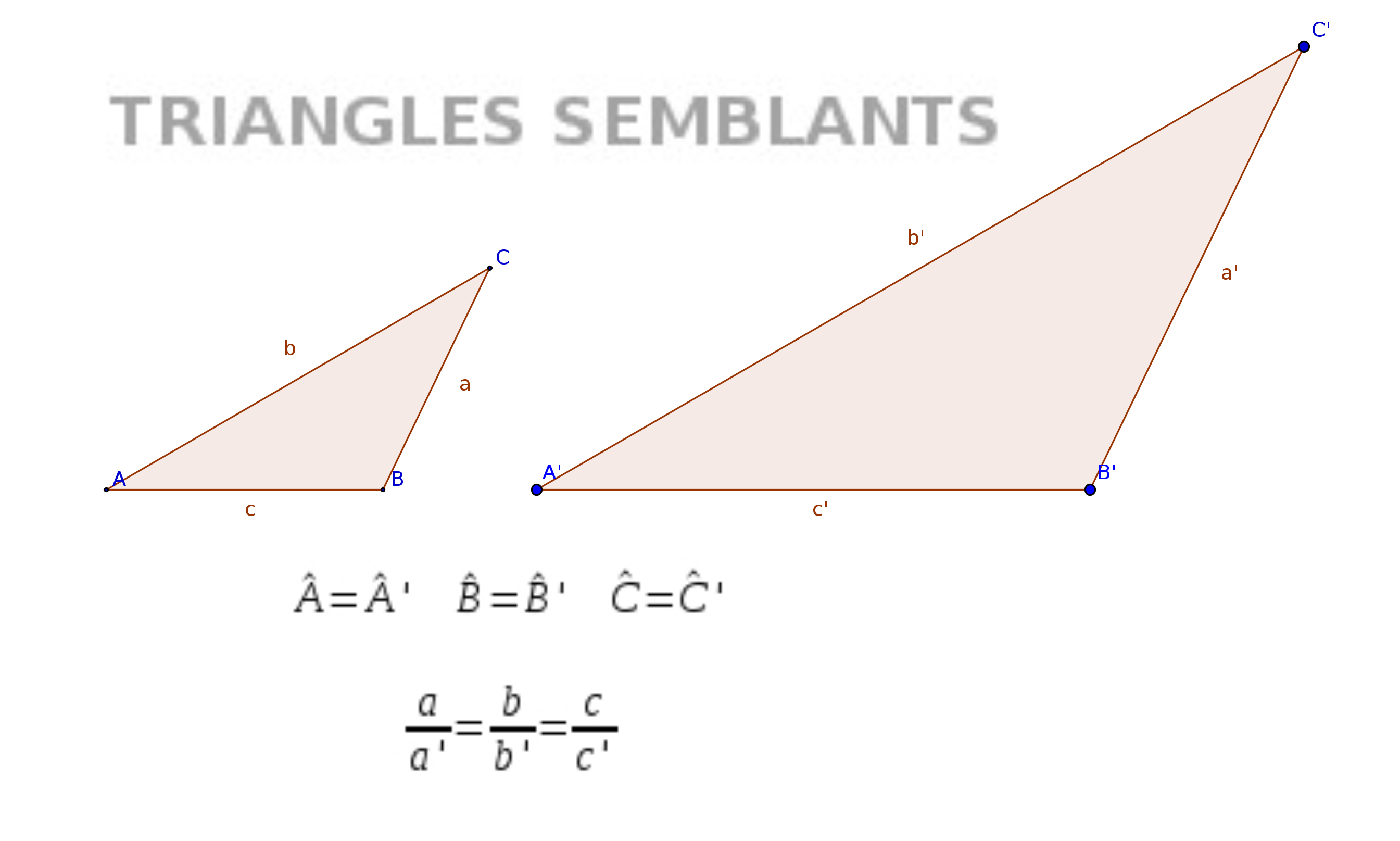
triangles-semblants




 

Un criteri de semblança de dos triangles és un conjunt de condicions que, si es verifiquen, permeten assegurar que els dos triangles són semblants.

No cal comprovar que els seus angles són iguals i que els seus costats són proporcionals per saber si dos triangles són semblants. N’hi ha prou que es verifiqui algun dels següents criteris:




Criteri 1: Tenen dos costats proporcionals i l’angle comprés igual.




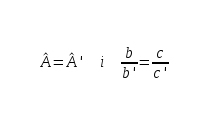
criteri1



Criteri 2: Els seus costats són proporcionals.




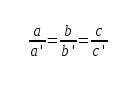
criteri2



Criteri 3: Tenen dos angles iguals.




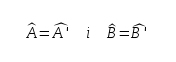
criteri3

 



Aquestos criteris són suficients per a comprovar que dos triangles són semblants.

Ara bé, qualsevol relaxació en un dels criteris comportaria l’incompliment e insuficiència a l’hora de verificar que els triangles són semblants i, per tant apareixerien contraexemples.


EXEMPLE: Vegem una relaxació en el criteri 1. 


Considerem dos triangles que tenen dos costats proporcionals i un angle igual. Però aquest angle no és l’angle comprés entre els dos costats.

Aleshores els triangles no són necessariament semblants.

 

 

Categoría: Semblança | DEJA UN COMENTARIO
septiembre 25

Probabilitat de repetir un element en una extracció amb reposició.

L’altre dia anava jo corrent pels horts del terme de Palma de Gandia amb els auriculars a les orelles i un CD reproduïnt-se aleatòriament, quan de cop i volta vaig començar a pensar.

Quina serà la probabilitat que en aquest moment es repetisca una cançó d’entre les que hi ha al CD.

És més, quina és la probabilitat de repetir una cançó per primera vegada en un moment determinat: en la segona elegida, en la tercera elegida, etc…

Una cosa tenia clara, si hi havia N cançons en el CD, aleshores:

Si X=n        significava que repetíem per primera vegada una cançó en la elecció n-èssima, tindríem que:

P( X = 1 ) = 0 P( X = N + 2 ) = 0

si el CD disposava de un total de N cançons.

És a dir era directament impossible repetir per primera vegada una cançó en la primera que escoltarem perquè no hi havia cap possibilitat de repetir.

A més a més, si escoltavem totes les cançons sense repetir-ne cap, a la següent segur que repetiriem ( per a X = N + 1 ) amb lo qual seria impossible repetir per primera vegada en l’elecció N + 2.

Però bé, vegem totes les probabilitats:

P ( X = 2 ) = \frac{1}{N} P ( X = 3 ) = \frac{N-1}{N} \frac{2}{N} P ( X = 4 ) = \frac{N-1}{N} \frac{N-2}{N}\frac{3}{N} P ( X = 5 ) = \frac{N-1}{N} \frac{N-2}{N}\frac{N-3}{N}\frac{4}{N} P ( X = n ) = \frac{N-1}{N} \frac{N-2}{N} \; \;\; \; \frac{N+2-n}{N}\frac{n-1}{N} P ( X = N ) =\frac{N-1}{N} \frac{N-2}{N} \; \;\; \; \frac{2}{N}\frac{N-1}{N} P ( X = N + 1 ) =\frac{N-1}{N} \frac{N-2}{N} \;\;\; \; \frac{2}{N}\frac{1}{N}

Per tant tindrem per al cas general:

Probabilitat del cas general
Probabilitat del cas general

Fes clic per a continuar llegint

Categoría: Estadística i probabilitat | Comentarios desactivados en Probabilitat de repetir un element en una extracció amb reposició.
septiembre 17

Càlcul del m.c.d. i el m.c.m. 2. Descomposició múltiple

Abans vam veure com calcular el m.c.d. i el m.c.m. mitjançant l’algorisme d’Euclides.

Passem ara a veure un mètode alternatiu però eficaç. En el qual mitjançant una única descomposició múltiple ( de tots els nombres a estudiar ) podem trobar de forma sencilla el m.c.d. i el m.c.m.

La idea és anar factoritzant tots els nombres a la vegada, on si un factor no divideix el nombres aleshores aquest es queda igual.

Però un EXEMPLE serà sempre millor que MIL PARAULES.

Vegem:

A. Calcula el m.c.d. i el m.c.m. de 132 i 120:

Primer exemple
PRIMER EXEMPLE

B. Calcula el m.c.d. i el m.c.m. de 1.032 i 180:

segon exemple
SEGON EXEMPLE

Categoría: 1r ESO, Divisibilitat | DEJA UN COMENTARIO
septiembre 4

Càlcul del m.c.d. i el m.c.m. 1. Algoritme d’Euclides.

ALGORISME D’EUCLIDES.

En principi la paraula algorisme és nova per a la majoria de nosaltres i ben bé podria esporuguir-nos o atabalar-nos, però vegem que diu el diccionari de la palabra algorisme.

ALGORISME: Procediment de càlcul que consisteix a acomplir un seguit ordenat i finit d’instruccions que condueix, un cop especificades les dades, a la solució que el problema genèric en qüestió té per a les dades considerades.1

Aleshores l’algorisme d’Euclides no és més que això: Una sèrie d’instruccions que dutes a terme porten a la solució del problema, és a dir, obtenim el m.c.d. de dos nombres.

Quines són les instruccions del algorisme d’Euclides per a trobar el m.c.d. de dos nombres donats:

PRIMER: Es divideix el número major entre el número menor.

SEGON: Si:

— La divisió és exacta, el divisor és el m.c.d.

— La divisió no és exacta, dividim el divisor entre el residu obtingut i contínuem de nou amb el pas segon fins que la divisió siga exacta.

ALESHORES, L’últim divisor será el m.c.d.

Després, com sabem que m.c.m.(a,b) x m.c.d.(a,b) = a x b

calcularem m.c.m.(a,b) amb la divisió:

EXEMPLES:

Fes clic per a continuar llegint

Categoría: 1r ESO, Divisibilitat, Sin categoría | DEJA UN COMENTARIO