TALLER DE GEOGEBRA (1)
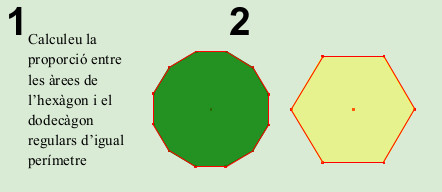
1.- Calculeu la proporció entre les àrees de l’hexàgon i el dodecàgon regulars d’igual perímetre.
RESOLUCIÓ AMB GEOGEBRA: «Algoritme geomètric».
0.) PREPAREM LA FINESTRA GRÀFICA:
Amb el botó dret damunt la finestra gràfica,
Desmarquem les caselles dels EIXOS i la GRAELLA
1.) DEFINIM EL VALOR «PARAMÈTRIC» DEL PERÍMETRE:
Cliquem en el penúltim menú damunt de «Punt lliscant«.
A continuació:
- Considerarem el paràmetre com a nombre.
- L’anomenarem a Nom: perímetre.
- A Interval considerarem des de 2 fins a 12 amb un increment de 0.1
(Observem que apareix un nombre amb el nom perímetre a la finestra algebraica)
Aleshores el valor del perímetre per a aquesta pràctica el farem variar de 2 fins a 12 amb un increment de 0,1.
2.) CREEM EL HEXÀGON REGULAR:
Cliquem en el tercer menú damunt de «Segment de longitud donada«.
Cliquem damunt de la finestra gràfica i apareixerà un menú que demana la «Longitud del segment«, introduïm: perímetre/6 i polsem en d’acord.
(Observem que apareixen els punts A i B i el segment f a la finestra algebraica)
Cliquem en el cinqué menú damunt de Polígon regular
Cliquem en els punts A i B del segment anterior.
Apareix un menú que demana pel nombre de vèrtexs del polígon regular.
Aleshores introduïm el valor 6 i polsem en d’acord.
(Observem que anomena la resta dels punts del hexàgon com C,D,E i F; i al polígon l’anomena pol1)
3.) CREEM EL DODECÀGON REGULAR: (Recordem que ha tenir el mateix perímetre del hexàgon regular).
Cliquem en el tercer menú damunt de «Segment de longitud donada«.
Cliquem a la finestra gràfica i apareix un menú que demana per la longitud del segment, introduïm el valor perímetre/12 i polsem en d’acord.
(Observem que apareixen els punts G i H).
Cliquem en el cinqué menú que damunt de Polígon regular
Cliquem en els punts G i H del segment anterior.
Apareix un menú que demana pel nombre de vèrtexs del polígon regular.
Aleshores introduïm el valor 12 i polsem en d’acord.
(Observem que anomena la resta dels punts del hexàgon com I,J,K,L,M,N,O,P,Q,R; i al polígon l’anomena pol2)
4.) FORMATEM EL RESULTAT.
A la finestra algebraica cliquem amb el botó dret sobre el nom pol1 i cliquem en «canvia el nom«.
Aleshores en Nou nom per al polígon pol1 escrivim HEXÀGON.
Fem el mateix amb pol2 i l’anomenem DODECÀGON.
A la finestra algebraica on apareix el títol Finestra algebraica punxem en el triangle que hi ha allí i de les tres icones que apareixen punxem a la primera.
Aleshores apareixen tots les objectes de la construcció a la finestra algebraica:
- Un nombre: perímetre.
- Dos polígons: HEXÀGON I DODECÀGON.
- Divuit punts: A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R.
- vint segments.
Cliquem sobre el punt A i amb la tecla MAJÚSCULES polsada cliquem sobre el punt R. Aleshores tots els punts quedaran seleccionats.
Polsem amb el botó dret sobre ells i desmarquem la opció «Mostra objecte«.
Despareixen tots els punts de la finestra gràfica.
Fem el mateix amb tots els segments.
5.) REDACTEM EL RESULTAT.
Escrivim a la casella d’entrada:
Areahexagon=Àrea[HEXÀGON]
Areadodecagon=Àrea[DODECÀGON]
RESULTAT=Areahexagon/Areadodecagon
Punxant a la finestra algebraica damunt de RESULTAT i sense soltar el ratolí arrosseguem fins a la finestra gràfica.
I tenim el resultat escrit a la finestra gràfica.
Com podem comprovar, per molt que canviem el valor del perímetre la proporció no canvia.
Finalment donem format al resultat:
Punxem amb el botó dret sobre el text del RESULTAT a la finestra gràfica, cliquem en propietats i aleshores:
A la pestanya color destriem un color per al text.
A la pestanya text destriem la font, el tamany i el posem en negreta.
Punxem amb el botó dret sobre la finestra gràfica, cliquem en la finestra gràfica i en la pestanya bàsic a l’apartat Miscel·lània destriem el color de fons desitjat.
VIDEO IL·LUSTRATIU:
Vegem un video en el qual es desenvolupa tota la construcció amb geogebra.