febrero
5
Dos
A quin nombre equival:
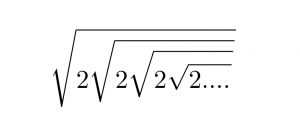
Si observem:
Si 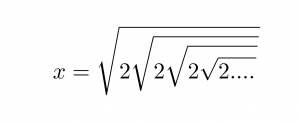
tenim que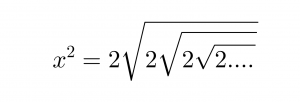
d’on 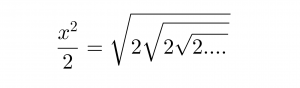
I per tant: 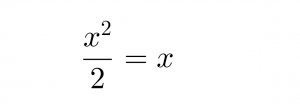
es a dir: 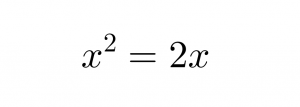
Sortint l’equació de segon grau: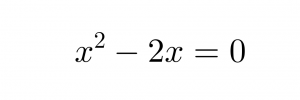
Que només té dues solucions 2 i 0. Com està clar: zero no pot ésser; per tant la solució és 2
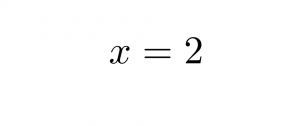
Considerem la següent taula on podem apreciar com s’aproxima a 2 l’expressió que estavem estudiant: