Operacions amb polinomis per a tercer d’ESO.
Aci escriurem el polinomio
Genera un polinomi de grau 6 i anomena'l P(x).
Genera un altre polinomi de grau 6 i anomena'l Q(x).
Genera un polinomi de grau 2 i anomena'l R(x).
Genera un polinomi de grau 4 i anomena'l S(x).
EXERCICI 1: Considera els polinomis anteriors i calcula:
A) P(x)+Q(x) i anomena'l A(x)
B) P(x)-Q(x) i anomena'l B(x)
C) 2·P(x)+3·Q(x) i anomena'l C(x)
D) 4·S(x)-A(x)-B(x) i anomena'l D(x)
EXERCICI 2: Considera els polinomis anteriors i calcula:
E) R(x) · S(x) i anomena'l E(x)
F) B(x) · S(x) i anomena'l F(x)
EXERCICI 3: Considera els polinomis anteriors i calcula:
G) S(x):(x2-2x+1) i anomena G(x) al quocient
H) A(x):(x-4) per Ruffini i anomena H(x) al quocient
EXERCICI 4:
I)Quants termes té el polinomi A(x), de quin grau és i quin és el seu terme independent.
J)Quants termes té el polinomi H(x), de quin grau és i quin és el seu terme independent.
Aqui teniu un exemple il·lustratiu.
Dos
A quin nombre equival:
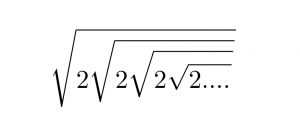
Si observem:
Si 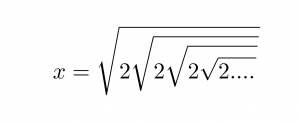
tenim que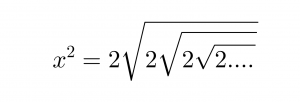
d’on 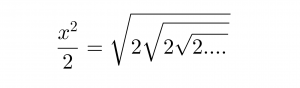
I per tant: 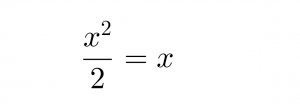
es a dir: 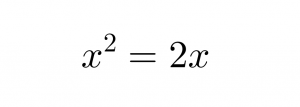
Sortint l’equació de segon grau: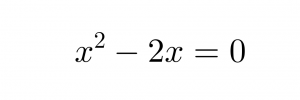
Que només té dues solucions 2 i 0. Com està clar: zero no pot ésser; per tant la solució és 2
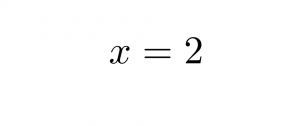
Considerem la següent taula on podem apreciar com s’aproxima a 2 l’expressió que estavem estudiant: