Probabilitat de repetir un element en una extracció amb reposició.
L’altre dia anava jo corrent pels horts del terme de Palma de Gandia amb els auriculars a les orelles i un CD reproduïnt-se aleatòriament, quan de cop i volta vaig començar a pensar.
Quina serà la probabilitat que en aquest moment es repetisca una cançó d’entre les que hi ha al CD.
És més, quina és la probabilitat de repetir una cançó per primera vegada en un moment determinat: en la segona elegida, en la tercera elegida, etc…
Una cosa tenia clara, si hi havia N cançons en el CD, aleshores:
Si significava que repetíem per primera vegada una cançó en la elecció n-èssima, tindríem que:
si el CD disposava de un total de N cançons.
És a dir era directament impossible repetir per primera vegada una cançó en la primera que escoltarem perquè no hi havia cap possibilitat de repetir.
A més a més, si escoltavem totes les cançons sense repetir-ne cap, a la següent segur que repetiriem ( per a X = N + 1 ) amb lo qual seria impossible repetir per primera vegada en l’elecció N + 2.
Però bé, vegem totes les probabilitats:
Per tant tindrem per al cas general:
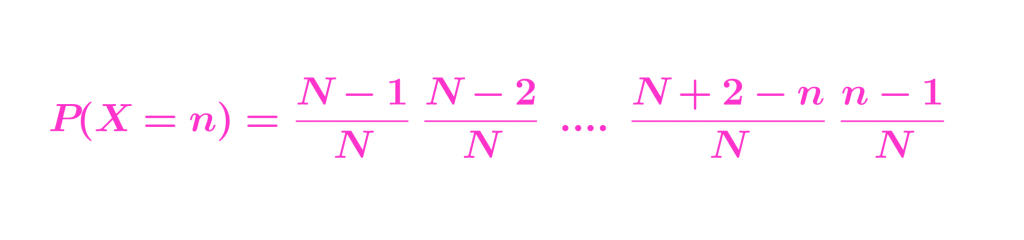
Vegem el cas en el que disposem de 5 cançons en el CD:
En la primera elecció:
En la segona elecció:
En la tercera elecció:
En la quarta elecció:
En la cinquena elecció:
En la sisena elecció:
A partir de la setena elecció: si n es major o igual a 7.
On podem observar que la suma:
Ja que: